√無料でダウンロード！ 分数関数 漸近線 求め方 244670-分数関数 漸近線 求め方

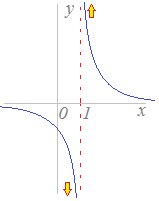
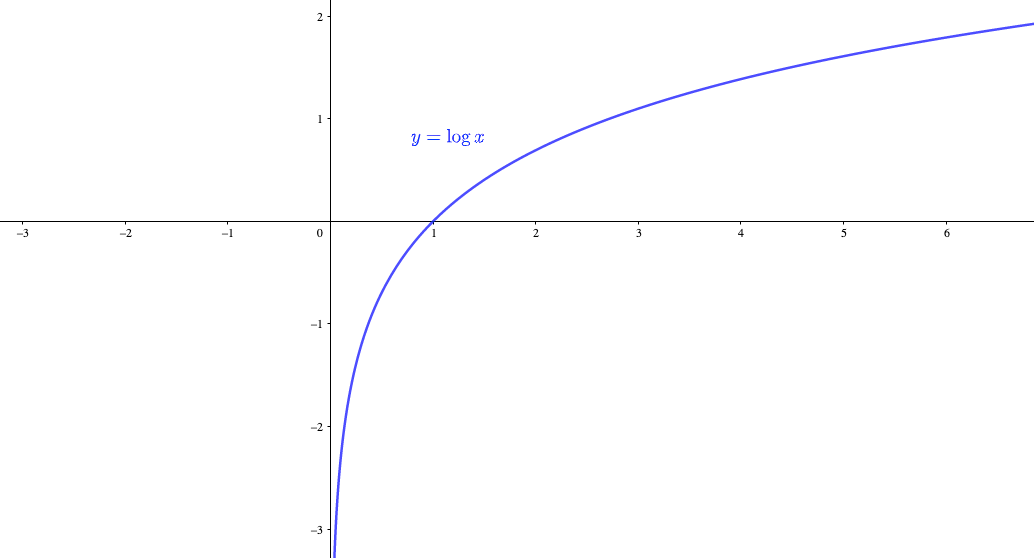
関数が定義されず， x→1 のとき y→±∞ となります．このとき， x=1 が漸近線になります．（図1．ただし，図1にはもう一つ横向きの（ x 軸に平行な）漸近線もありますが，これについては(2)で解説します．） 例12 y=tan x における x= ， y=log x における x=0 のようにここでは、逆関数を求める練習として、一次分数関数の逆関数を求めてみます。なお、一次分数関数は、基本一次分数関数で取り上げています。 一次分数関数の逆関数 次のような一次分数関数 f(x)= dfrac{2x1}3332(グラフの準備：漸近線の求め方(分数関数)) 19/11/2 2,231 ビュー 見てもらうために作成しておりますので，どんどん見てください．

漸近線についての質問です 微分のグラフを書くときの漸近線の求め方が分かり Yahoo 知恵袋

分数関数 漸近線 求め方

分数関数 漸近線 求め方-よってx→－∞、つまりグラフの左側の漸近線はy＝0となる。 このように分数関数だったり無理関数だったりすることで 求め方が少し変わってくると覚えるのは面倒になる。 考え方は同じだが、一問一問そうじっくり考えるのも面倒だ。 そこでやはり漸近線一次関数 式の求め方切片が与えられている （4）点(2,5)を通り、切片が3である直線 （2）とは逆で切片が与えられているけど、傾きが分からないというパターンの問題です。

漸近線の方程式

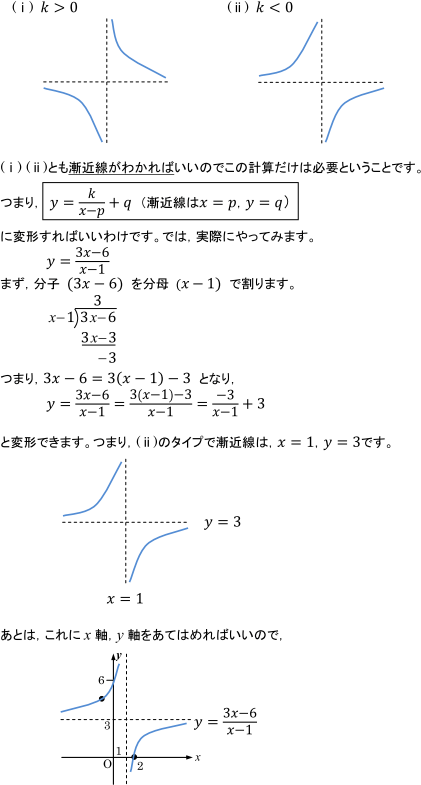
よってx→－∞、つまりグラフの左側の漸近線はy＝0となる。 このように分数関数だったり無理関数だったりすることで 求め方が少し変わってくると覚えるのは面倒になる。 考え方は同じだが、一問一問そうじっくり考えるのも面倒だ。 そこでやはり漸近線漸近線を考えるときには原点から遠い部分の関数の形を考えています。 そこで，大雑把な考え方ですが， x x x と y y y は 1 1 1 より十分大きい 部分での議論として， 右辺の 1 1 1 （または − 1 1 − 1 ）という定数項を無視してしまいます。に断りがない場合，分数関数の定義域は，分母を にする の値を除く実数全体である。 分数関数のグラフと性質 1 分数関数 \ n s t のグラフは， \ n のグラフを 軸方向に s，\ 軸方向に t だけ平行移動した直角双曲線で， 漸近線は 直線 s，\ t である。

漸近線の求め方を解説しました。 グラフの漸近線は、x軸に垂直な漸近線とそうでない漸近線とがあります。 そうでない漸近線は、\(x\to\pm\infty\)において漸近線と曲線が限りなく近づきます。 漸近線の方程式を\(y=axb\)とすると、曲線\(y=f(x)\)の漸近線は、こんにちは、ウチダショウマです。 今日は、数学Ⅱで初めて登場するが詳しくは数学Ⅲで習う 「漸近線」 について、求め方、意味、定義について解説していきます！ 主な具体例(分数関数や双曲線)も挙げながら詳しく見ていきましょう♪ 漸近線とは まずは聞き慣れない言葉だと思いますので漸近線を考えるときには原点から遠い部分の関数の形を考えています。 そこで，大雑把な考え方ですが， x x x と y y y は 1 1 1 より十分大きい 部分での議論として， 右辺の 1 1 1 （または − 1 1 − 1 ）という定数項を無視してしまいます。

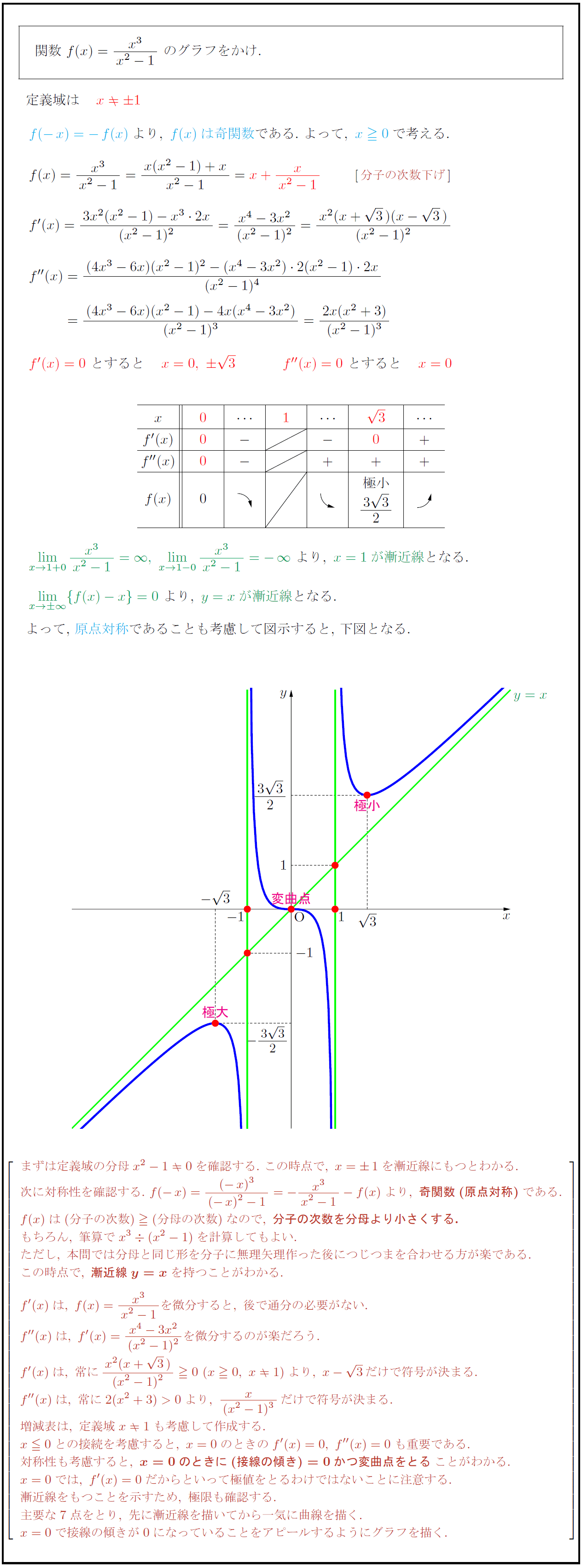
3332(グラフの準備：漸近線の求め方(分数関数)) 19/11/2 2,231 ビュー 見てもらうために作成しておりますので，どんどん見てください．Y=x/logxの関数なのですが (3)から(8)が以下の通りで、 (9)が (9) グラフの概形をかけ極値を取る点と変曲点の座標および漸近線を記入することまた，(3)~(8) の結 果がグラフのどの部分に表れているかを明記することここでは、逆関数を求める練習として、一次分数関数の逆関数を求めてみます。なお、一次分数関数は、基本一次分数関数で取り上げています。 一次分数関数の逆関数 次のような一次分数関数 f(x)= dfrac{2x1}

漸近線の方程式

授業での雑談ネタ 怜悧玲瓏 高校数学を天空から俯瞰する

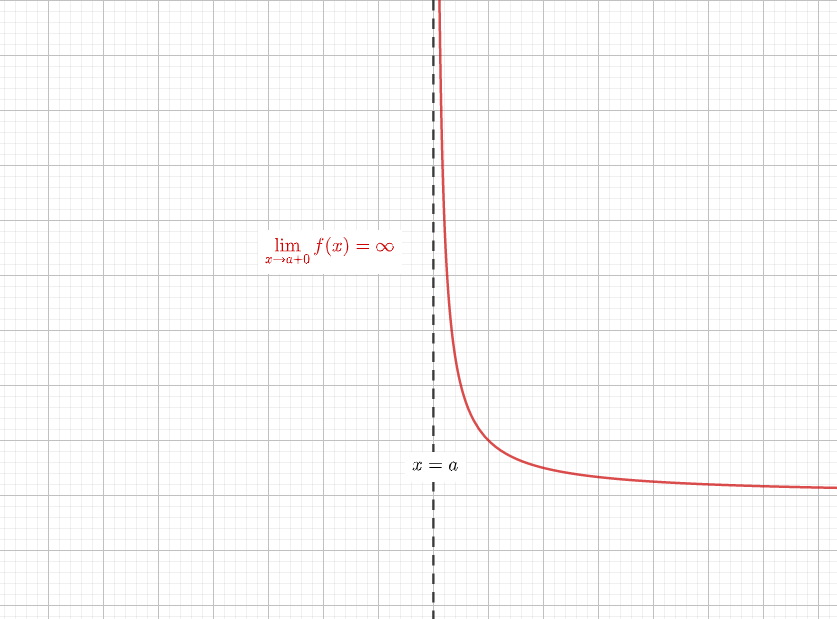
漸近線を考えるときには原点から遠い部分の関数の形を考えています。 そこで，大雑把な考え方ですが， x x x と y y y は 1 1 1 より十分大きい 部分での議論として， 右辺の 1 1 1 （または − 1 1 − 1 ）という定数項を無視してしまいます。Q 漸近線の求め方 初歩的な質問かもしれませんが、漸近線の導き出し方 がわかりません。たとえば、 y=x^2/(x2) の概形をかけ。 という問題で、増減表で凹凸を調べ、与式が y=x24/(x2)と変形されるところまでは理解できたのですが、漸近線をもつ関数のグラフをかくときは，漸近線を求める必要がある。漸近線についてまとめると以下のよ うになる。 (1) lim ( ) x f x a またはlim ( ) x f x a のとき直線y a は漸近線。 (2) 0 lim ( ) x p f x または 0 lim ( ) x p f x または 0 lim ( ) x p f x

Javascript Y軸に平行な漸近線を描く Mm参考書

分数関数

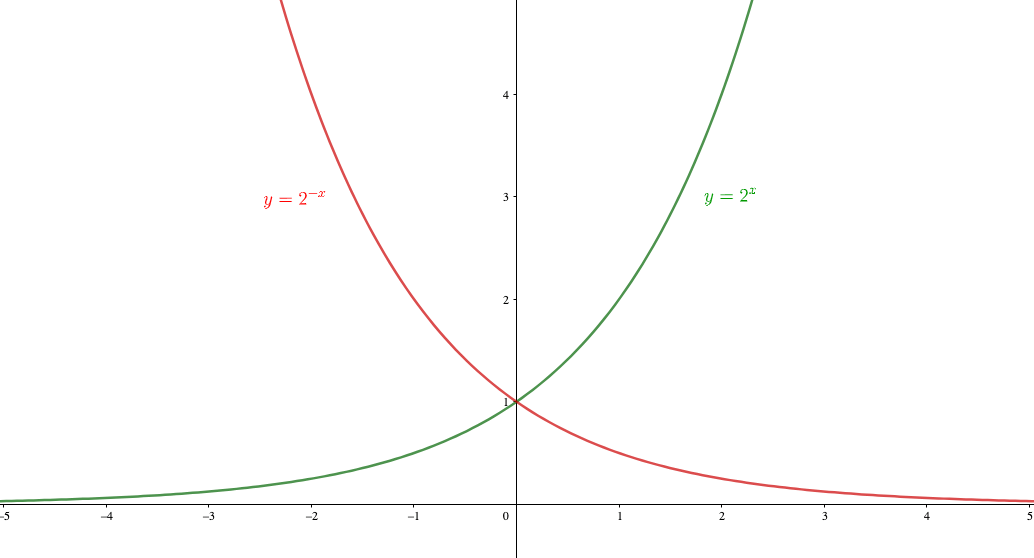
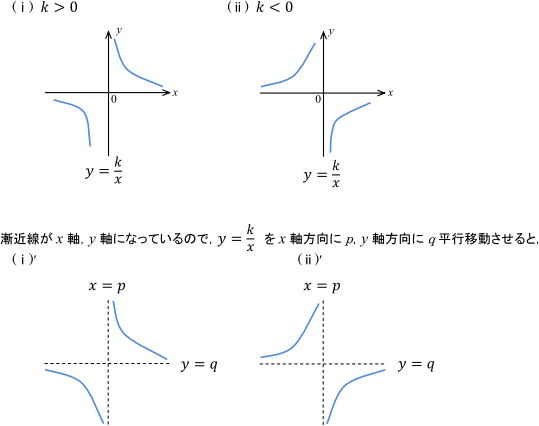
・双曲線の漸近線 →双曲線の漸近線の簡単な求め方と証明 ・二次曲線の平行移動 →グラフの平行移動の公式の証明と例 ・二次曲線と直線 ・二次曲線の離心率 円錐曲線 →二次曲線の分類（四通りの方法） ・媒介変数表示 ・サイクロイドこれから関数は、 （基本形）のグラフをx軸，y軸の正の方向へそれぞれp，qだけ平行移動したものである。 このときx＝p，y＝qが漸近線となる。ここで、 のグラフは、直線y＝xに関して対称なグラフであるから逆関数も である。 逆関数の漸近線はx＝q，y＝pより、その方程式は、 となる。漸近線を持つ代表的な関数 漸近線はない場合もありますし、複数ある場合もあります。 ですが漸近線を必ず持つとわかっている関数がいくつかあるので、最低限これらの関数は押さえておきましょう。 指数関数 \(y=2^x,y=2^{x}\)はグラフのようになりますが、\(x\)軸に着目すると漸近線である

標準 一次分数関数の逆関数 なかけんの数学ノート

漸近線 Wikipedia

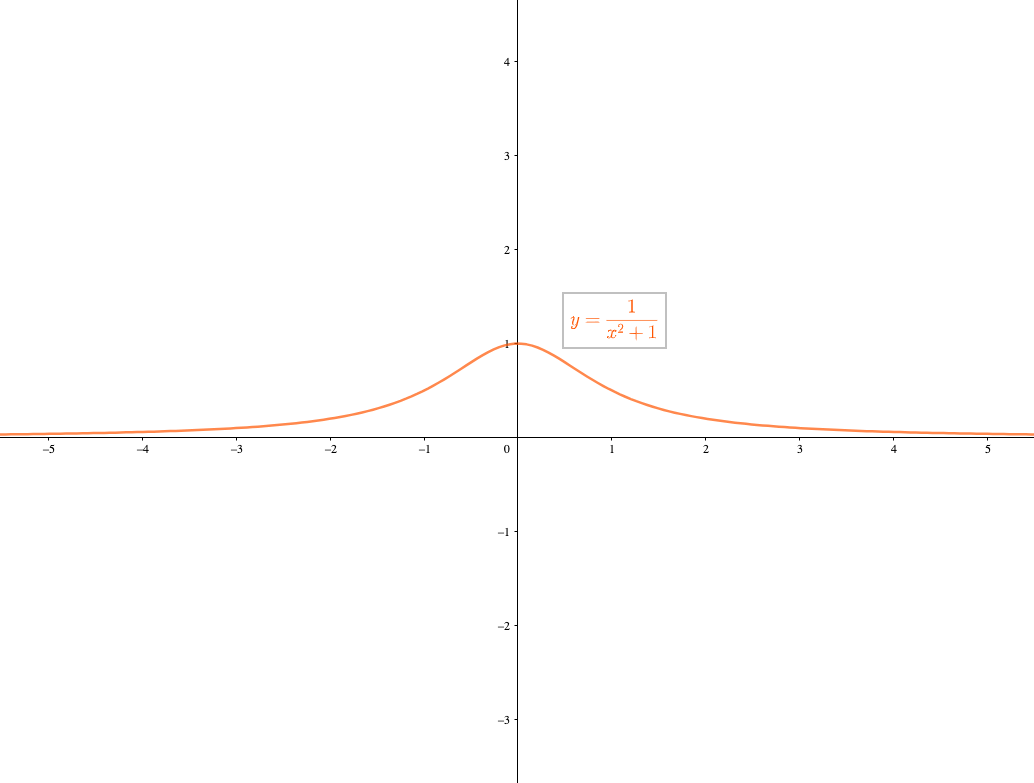
上野竜生です。今回は分数関数のグラフの書き方や定義域・値域・漸近線の求め方と、逆に定義域や漸近線がわかっているときの分数関数の求め方などについて紹介します。 \( \displaystyle y=\fracY=x/logxの関数なのですが (3)から(8)が以下の通りで、 (9)が (9) グラフの概形をかけ極値を取る点と変曲点の座標および漸近線を記入することまた，(3)~(8) の結 果がグラフのどの部分に表れているかを明記すること定数関数、多項式関数のグラフには、漸近線は存在しない。 漸近線が存在する最も簡単な例は、関数 f(x) = 1 / x のグラフである。 このグラフの漸近線は、直線 x = 0 と直線 y = 0 である。 グラフを描くと、曲線 y = 1 / x は x → 0±, x → ±∞ のときにそれぞれ y 軸、 x 軸に近づくことが見てとれる。

ウチダ 遊ぶ数学 新記事更新しました 漸近線の求め方や意味や定義とは 分数関数や双曲線 とは 分数関数 双曲線 定義 意味 求め方 漸近線 関数 T Co Jd0lnnfveo

数3の分数関数 解き方がわかりません 高校数学に関する質問 勉強質問サイト

例えば、y= x x/(x1)の関数の場合は、漸近線はy=xとx=1とわかりますが、y= x/(x^21)のように分母に二乗があるような場合は漸近線はどうなるのでしょうか？質問ばかりでもうしわけありませんが、 漸近線の求め方と x＝1近辺の極限の求め方ここでは、関数のグラフをかくときに必要となる、漸近線について見ていきます。 定義域の境目や端っこについて 例題 次の関数の増減、極値、凹凸、漸近線を調べて、グラフをかきなさい。 y=x dfrac{1}{x}

漸近線 Wikipedia

漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック

初歩的な質問ですいません Clear

漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック

漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学

漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック

数iii 微分 4 10 分数関数専用 極値の次数下げ公式の攻略 中級編 Youtube

分数関数のグラフの概形 書き方 高校数学 Youtube

漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学

高校数学 分数関数のグラフ １ 映像授業のtry It トライイット

2次 1次 型分数関数の動く範囲の素速い求め方 Den Of Hardworking

高校数学 分数関数のグラフ １ 映像授業のtry It トライイット

漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学

高校数学 分数関数のポイント整理 双曲線と漸近線 偏差値40プログラマー

分数関数y Bx C X Aのグラフは 点 1 3 を通り2直 Yahoo 知恵袋

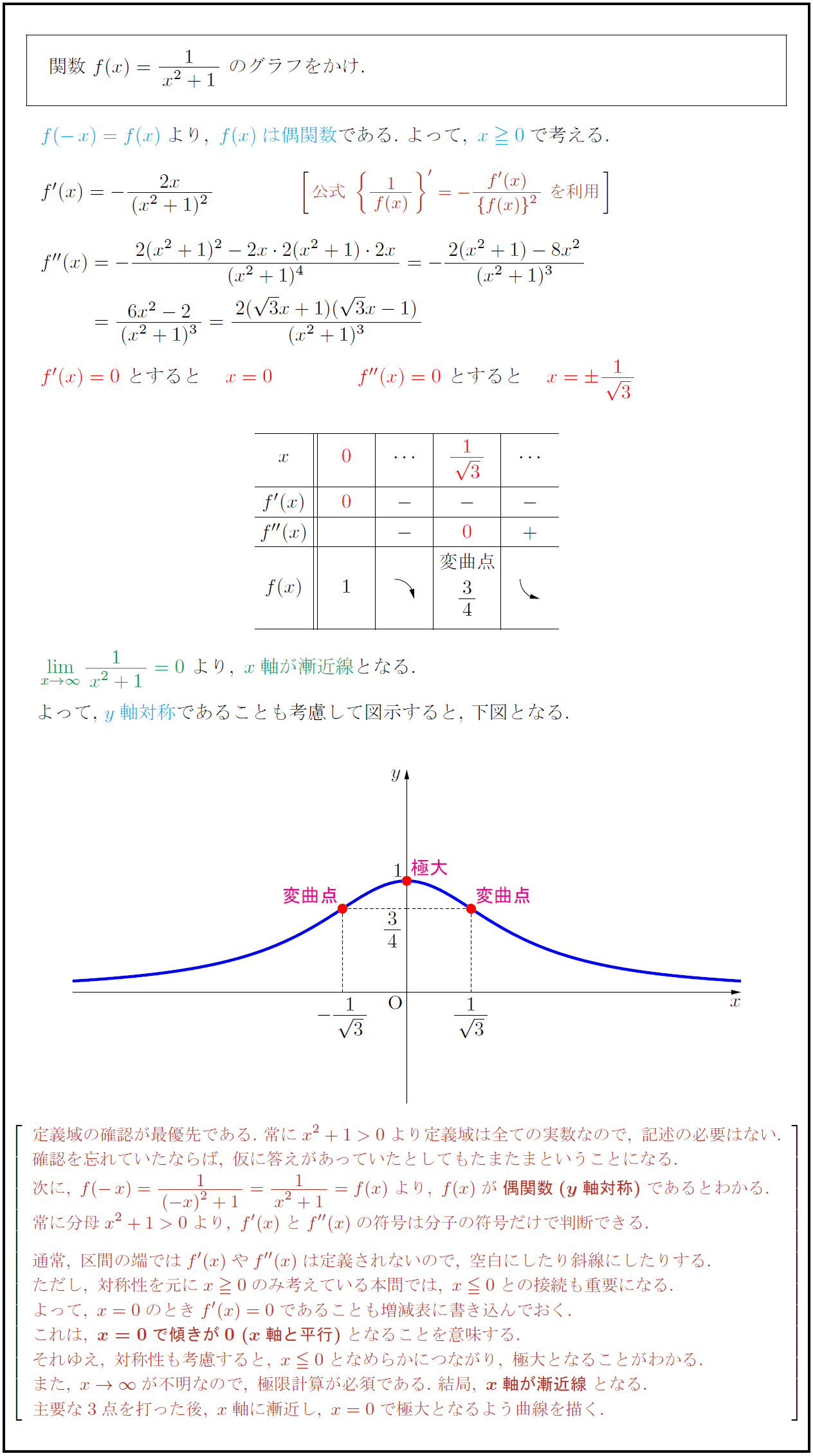
高校数学 分数関数 Y 1 X 1 のグラフ 受験の月

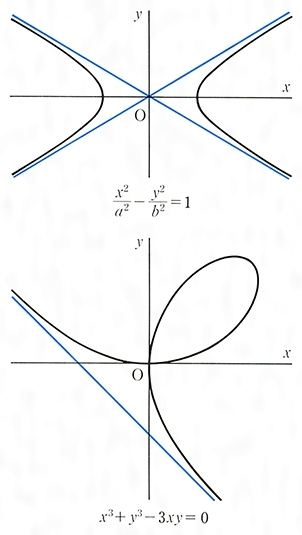
漸近線とは コトバンク

分数関数とは グラフや微分 積分 不等式の解き方 受験辞典

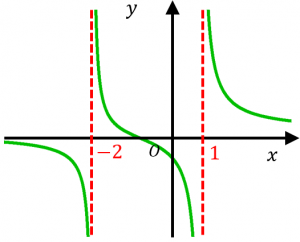
漸近線の求め方３パターン 具体例で学ぶ数学

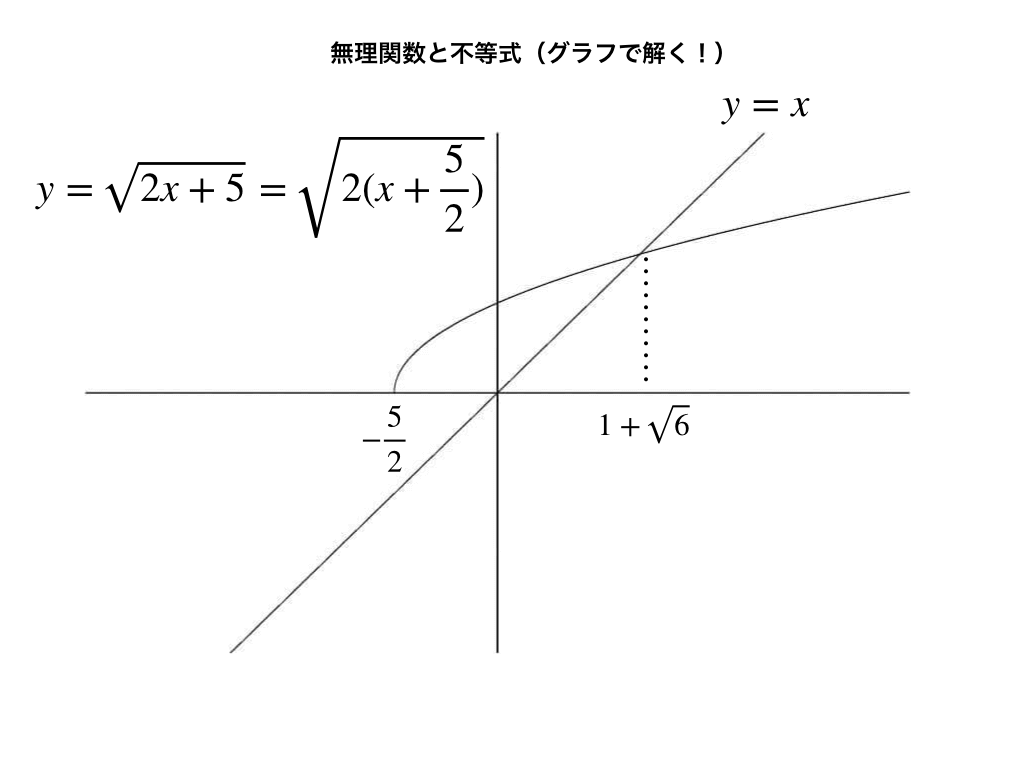
分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法

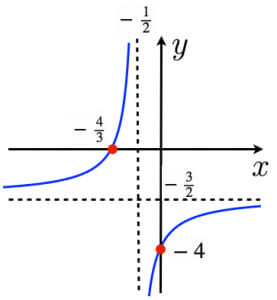
一次分数関数のグラフと漸近線 高校数学の美しい物語

漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学

分数関数の平行移動 数学iii By Okボーイ マナペディア

高校数学 分数関数のグラフについて教えてください 分数関数に限 Yahoo 知恵袋

漸近線 Wikipedia

漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学

漸近線の方程式

漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック

漸近線についての質問です 微分のグラフを書くときの漸近線の求め方が分かり Yahoo 知恵袋

高校数学 分数関数 Y X X 1 のグラフ 受験の月

高校 数学 関数２ 分数関数のグラフ２ ２１分 Youtube

分数関数のグラフ 三重の個人契約家庭教師

2次 1次 型分数関数の動く範囲の素速い求め方 Den Of Hardworking

漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学

高校数学 逆関数の求め方とグラフ 受験の月

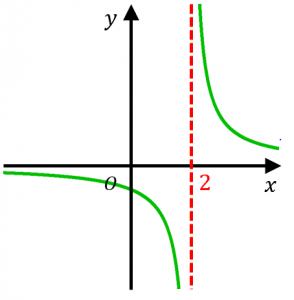
漸近線の求め方３パターン 具体例で学ぶ数学

基本 一次分数関数のグラフ なかけんの数学ノート

漸近線の描き方 一目瞭然早見チャート 高校生 数学のノート Clear

授業での雑談ネタ 怜悧玲瓏 高校数学を天空から俯瞰する

漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック

関数と極限 分数関数のグラフのかき方 数学 定期テスト対策サイト

標準 微分と関数のグラフと漸近線 なかけんの数学ノート

関数と極限 分数関数のグラフのかき方 数学 定期テスト対策サイト

高校数学 グラフのかき方 ２ 問題編 映像授業のtry It トライイット

漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック

高校数学 1次分数関数の決定 受験の月

分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法

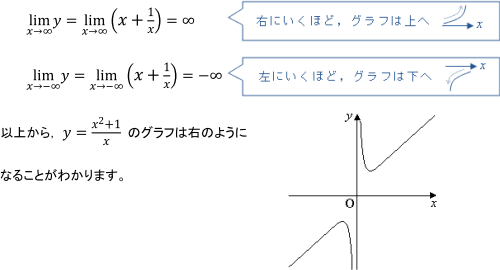
複雑な関数のグラフのかき方 数学 苦手解決q A 進研ゼミ高校講座

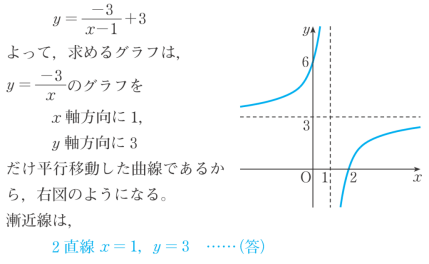
関数と極限 分数関数のグラフのかき方 数学 定期テスト対策サイト

高校数学 分数関数のグラフと漸近線以下の問題を解いていたら漸近線 Yahoo 知恵袋

分数関数とは グラフや微分 積分 不等式の解き方 受験辞典

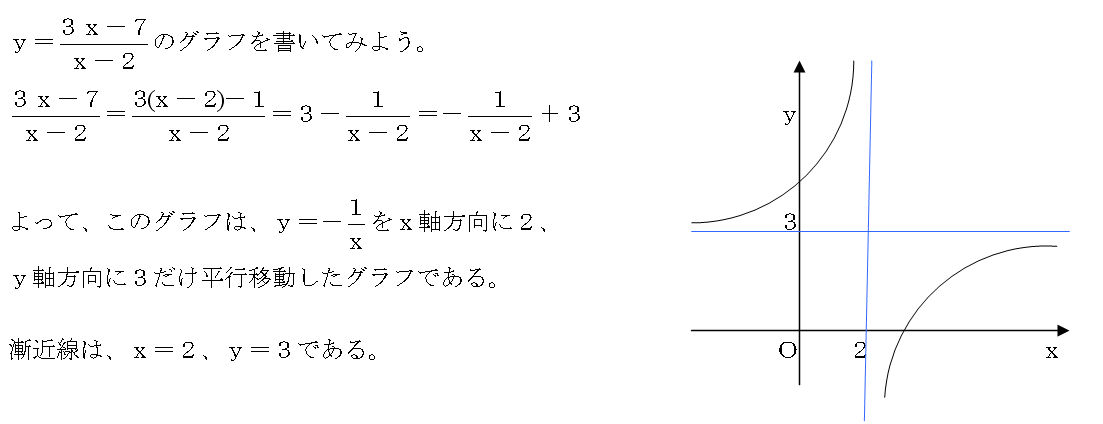
分数関数のグラフで計算変形がいる場合の問題 三重の個人契約家庭教師

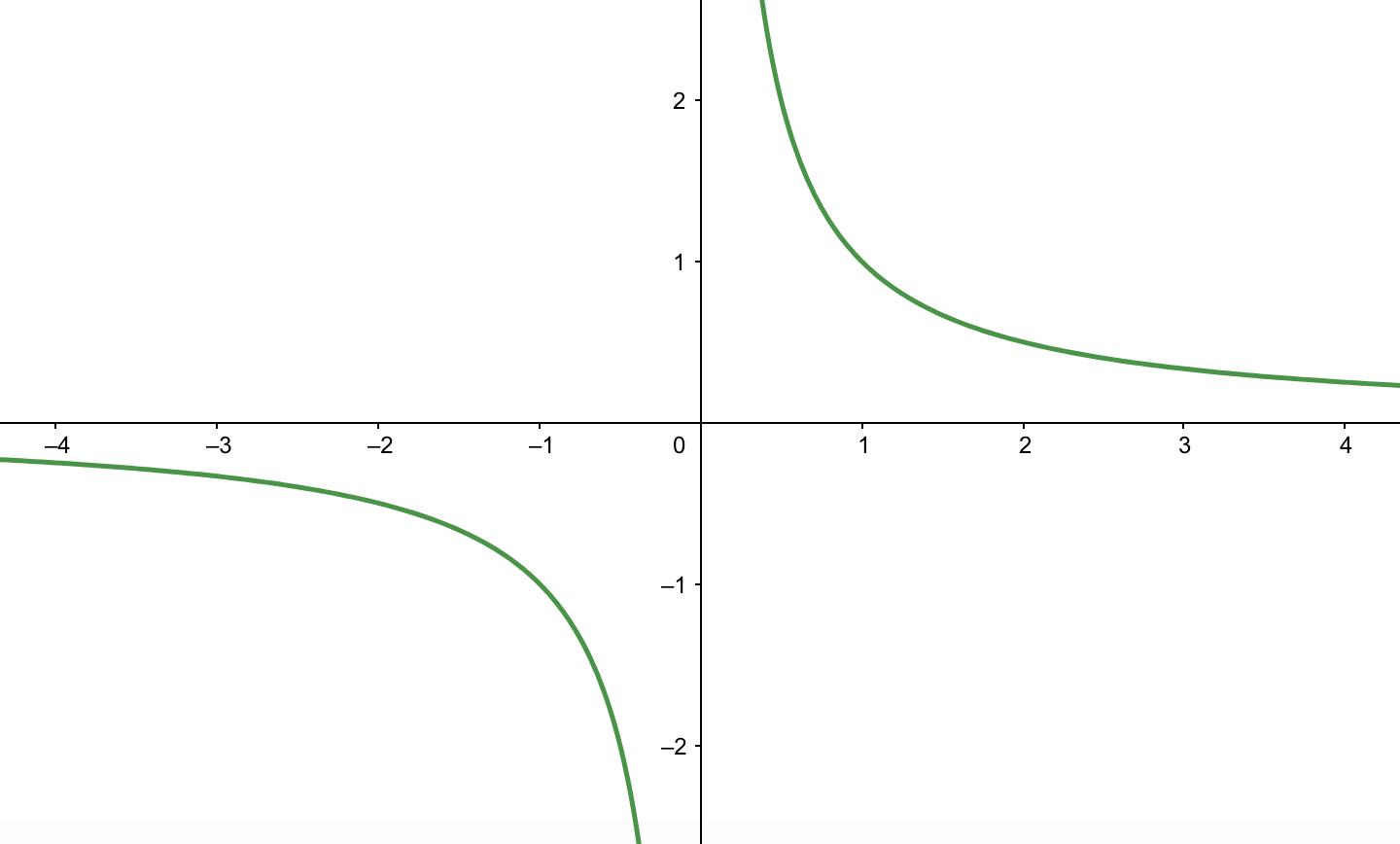
漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック

分数関数のグラフと漸近線 高校数学 関数 １ Youtube

漸近線 Wikipedia

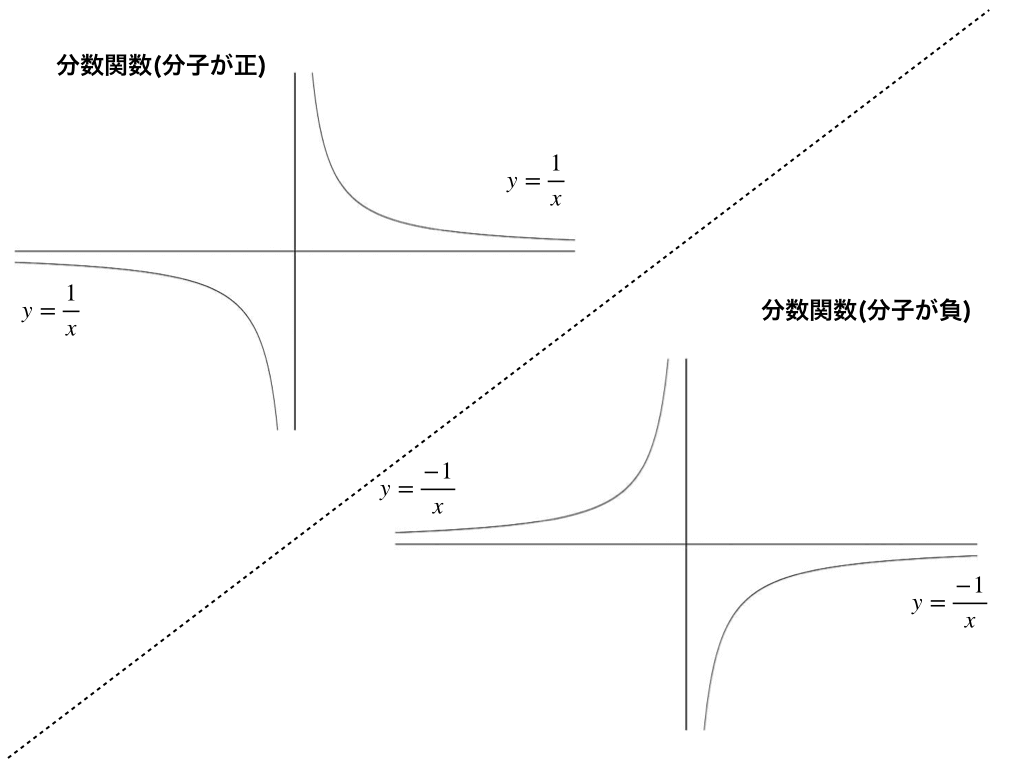
分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法

だいたい分かりますが ウ では除く点があるのに ア イ 高校数学に関する質問 勉強質問サイト

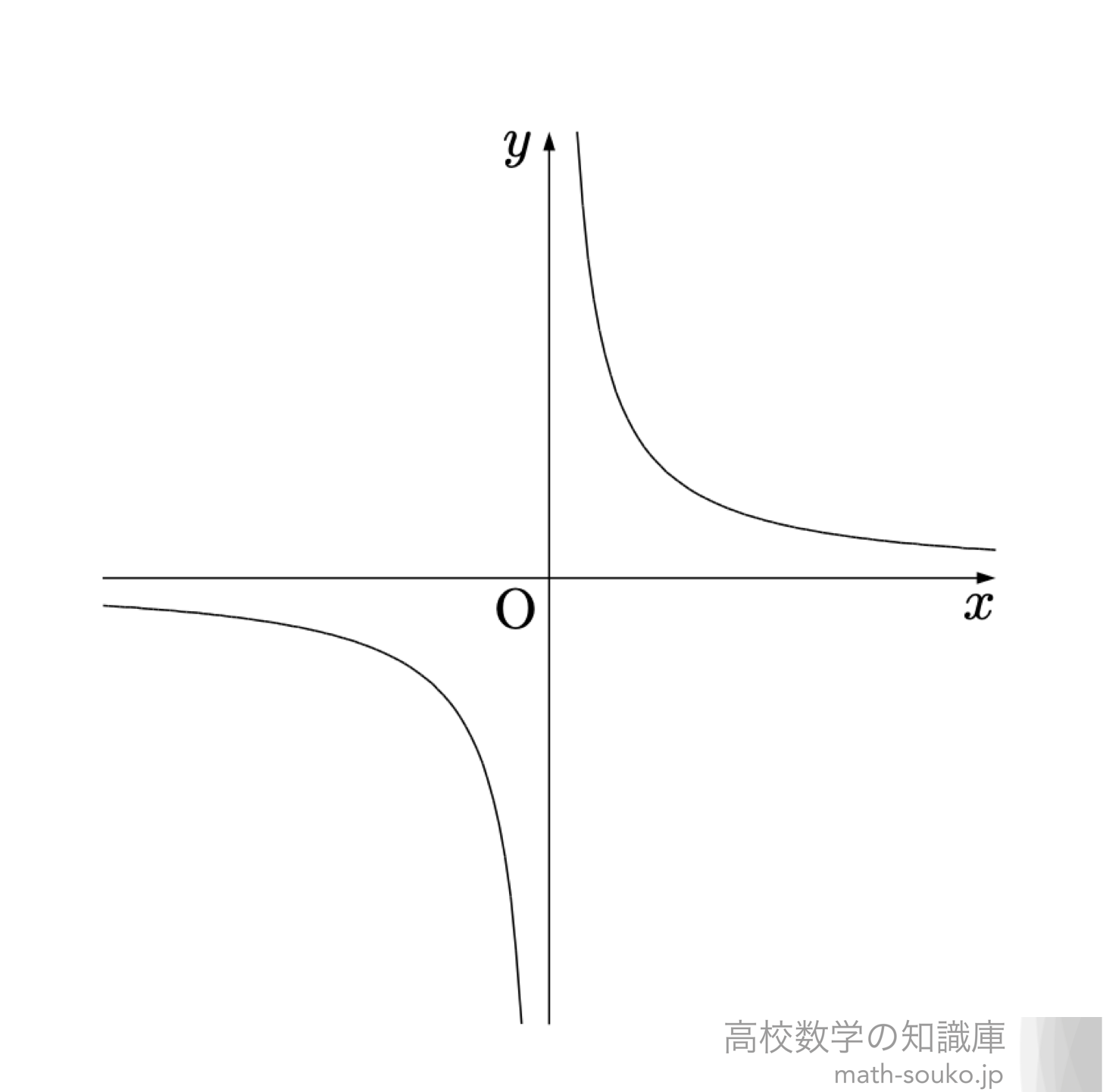
分数関数のグラフ 反比例と平行移動 高校数学の知識庫

関数の漸近線を求める方法なんですけど したの画像のように式変形しないと Yahoo 知恵袋

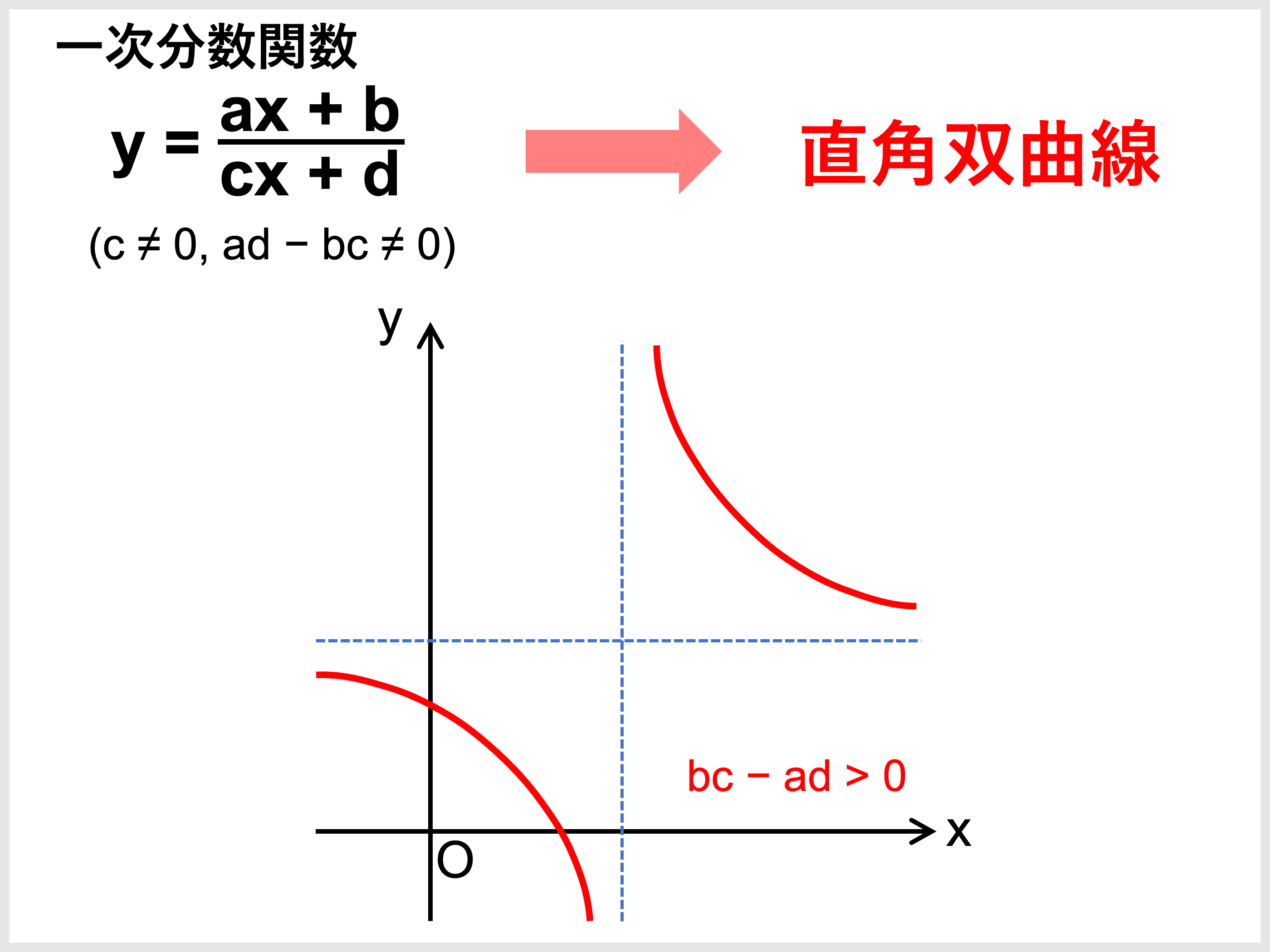
分数関数とは グラフや微分 積分 不等式の解き方 受験辞典

基本的な事は分かります かっこ2の問題で下線部のところがなぜ 高校数学に関する質問 勉強質問サイト

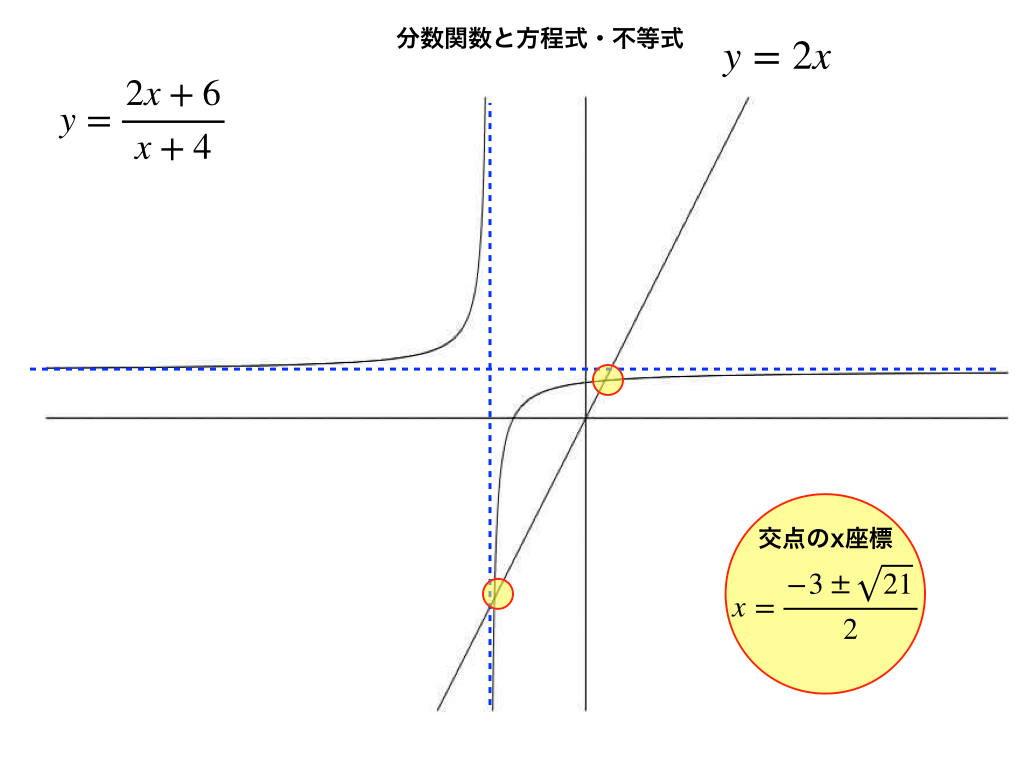
分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法

分数関数とは グラフや微分 積分 不等式の解き方 受験辞典

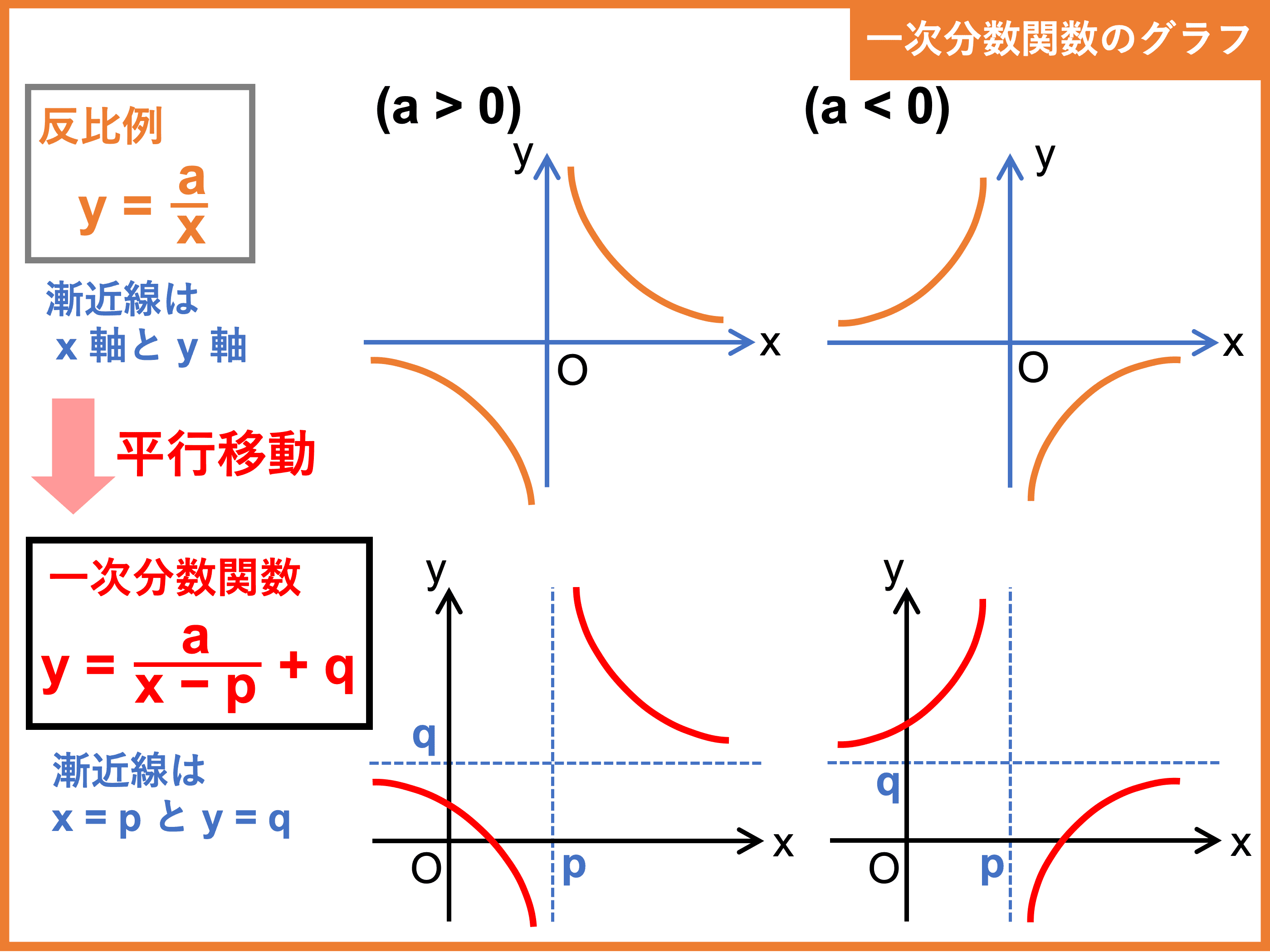
分数関数とは グラフや微分 積分 不等式の解き方 受験辞典

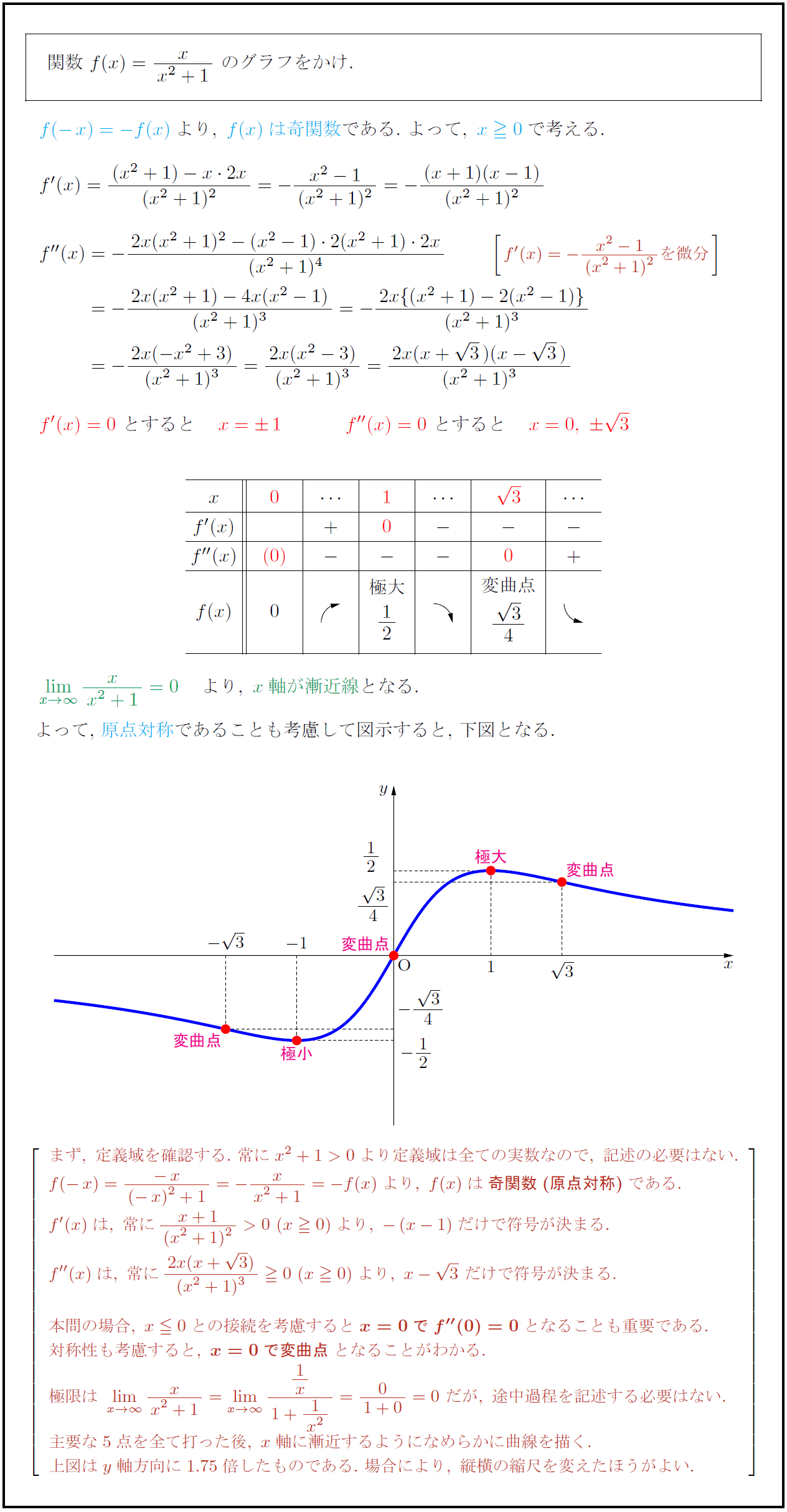
高校数学 分数関数 Y X X 1 のグラフ 受験の月

漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック

分数関数のグラフについて 分母が一次関数の時は理解できます 高校数学に関する質問 勉強質問サイト

分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法

一次分数関数のグラフと漸近線 高校数学の美しい物語

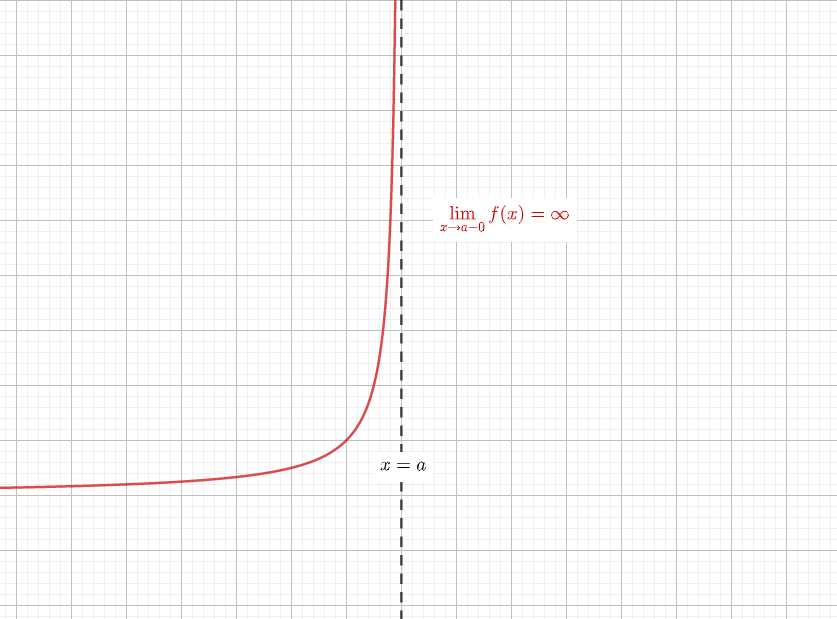
漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック

漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学

分数関数のグラフの書き方 定義域 漸近線 数学の偏差値を上げて合格を目指す

高校数学 分数関数のグラフ ２ 映像授業のtry It トライイット

分数関数の漸近線の求め方は分かるのですが 直角双曲線の求め方が分 Yahoo 知恵袋

高校数学でお願いします 漸近線について 分数関数の分母 0なるよう Yahoo 知恵袋

漸近線の求め方 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc

Studydoctor分数関数のグラフの書き方 高校数学 Studydoctor

標準 一次分数関数の逆関数 なかけんの数学ノート

漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学

漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学

分数関数のグラフ 反比例と平行移動 高校数学の知識庫

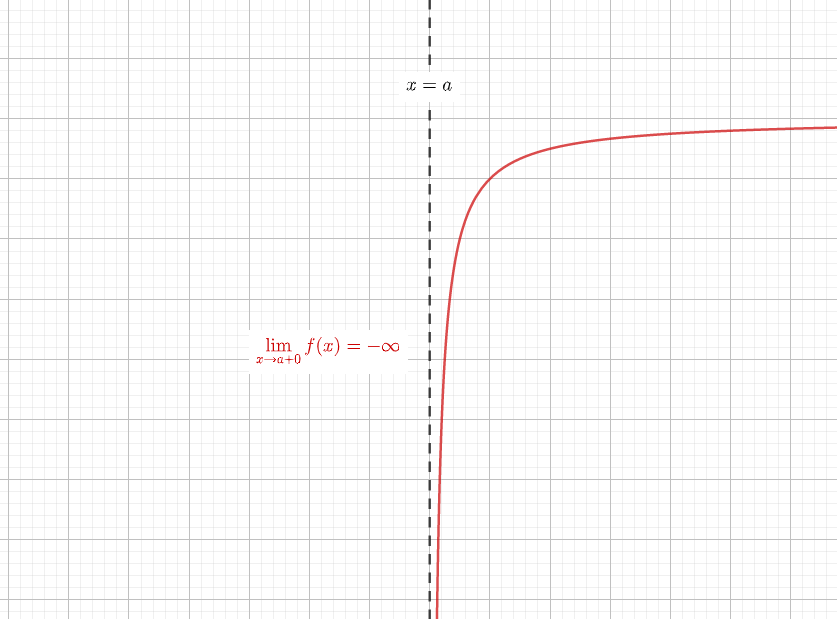
漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック

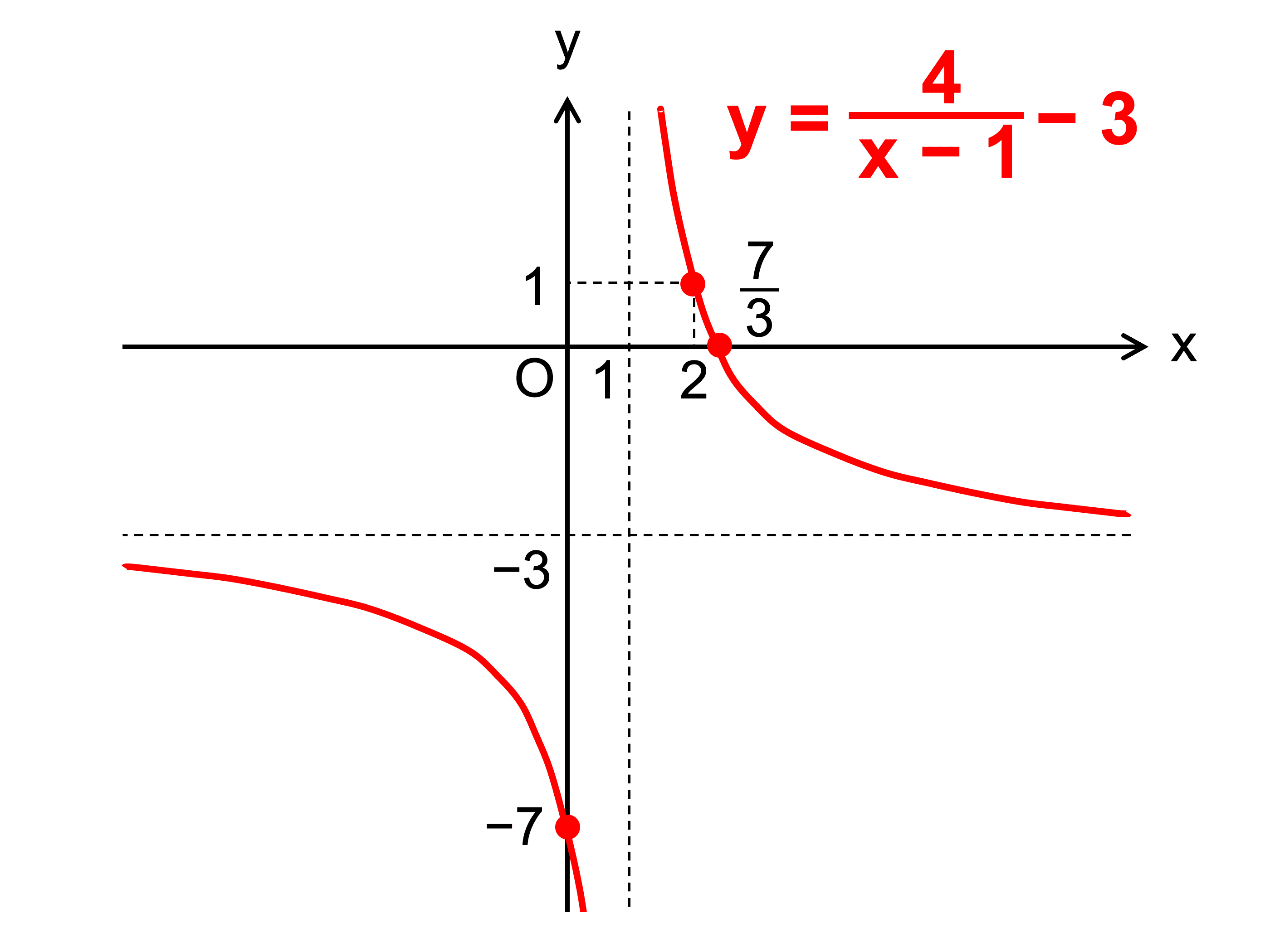
分数関数とは グラフや微分 積分 不等式の解き方 受験辞典

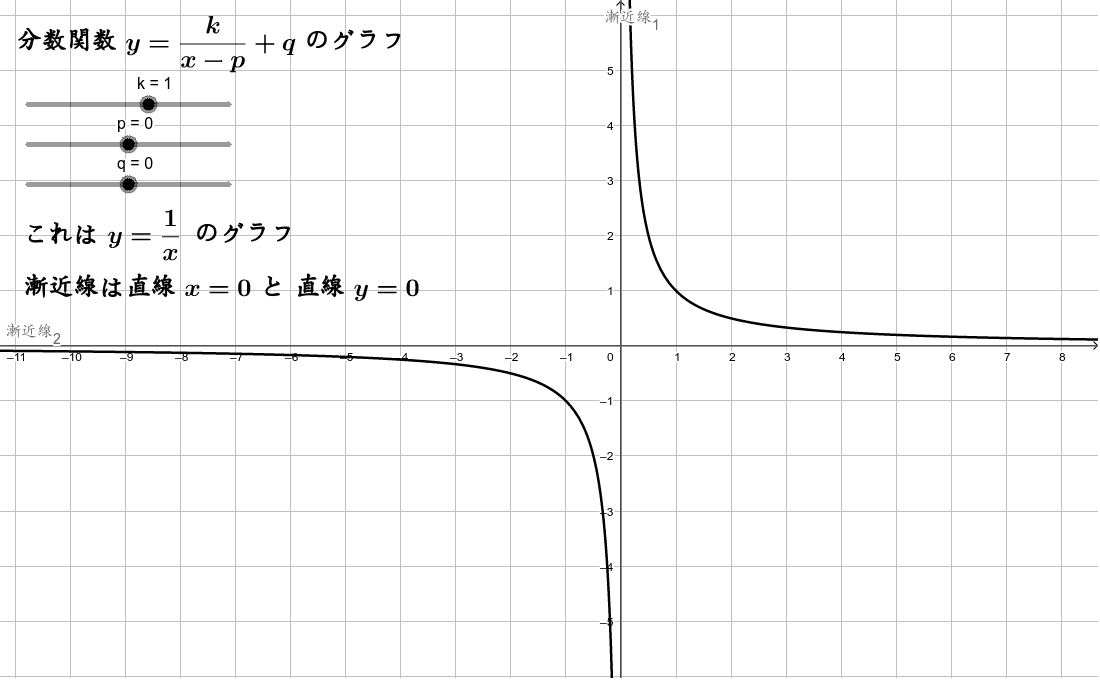
分数関数のグラフ Geogebra

Y Ax B 2x 1 1 のグラフが点 1 0 Okwave

高校数学の数3の漸近線の求め方なのですが なぜ括弧の中のような事 Yahoo 知恵袋

標準 一次分数関数の逆関数 なかけんの数学ノート

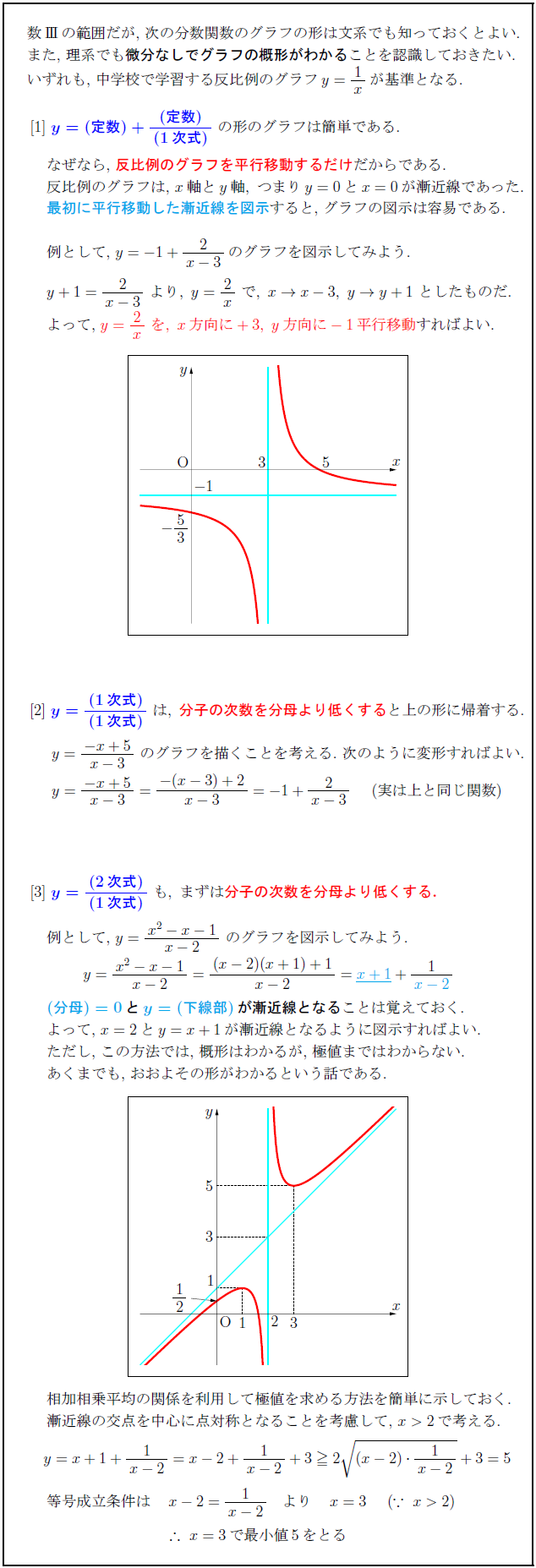
高校数学 文系も知っておくべき基本的な分数関数 数 のグラフ 受験の月

分数関数のグラフと漸近線 高校生 数学のノート Clear

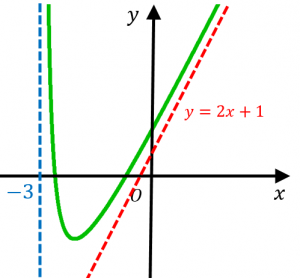
漸近線の求め方３パターン 具体例で学ぶ数学

Incoming Term: 分数関数 漸近線 求め方,